要約
誤差の指標は多々ありますが、それらを仮想のデータを用いて比較してみました
比較した指標はME・MAE・MSE・RMSE・MPE・MAPE・RMSPEの7つ。
それぞれを比較すると、ME・MPEは理論値/予測値と測定値の差が正になるか、負になるかの影響を受ける_点で、他の指標とは異なります。また、比例誤差では、比例するのであればBaseや例数の影響を受けないという特性がありますが、これは加速度的に影響を受けるのであれば、影響を受けるはずです。
ですので、数字だけで判断するのは難しそう・・・
可能であれば指標を使いつつ、実際にグラフを作成するなど可視化することの方が正確性が増し良い結果となると思います。
まえおき
薬剤師をしていると、腎機能の評価は必須(と思っていますが、私だけだったらどうしよう⋯⋯)
腎機能の評価にはeCCrやeGFRなど、腎機能の推算式を使って評価するのが一般的です。これらの論文を見てみるとMEやらMAEやら出てきて分かりにくい。ですので、実際に仮想のデータを用いて、どのように数字が動くか、確認してみました。
今回の検討は正確性を期して作成しておりますが、間違えなどがありましたら教えていただけたらと思います。コメントは私が行った後の感想・考察になります。これらの使用・解釈はそれぞれの方が自己責任でお願いします。
誤差の指標
下記7つについて確認していきます。まずはそれぞれがどのような数値/指標か確認していきましょう。
ちなみに下記以外にMASE(平均絶対スケーリング誤差)など他にもあります。
記号は下記とします。
n:データ数
i:データの順番。i番目のデータってこと
y:実測値/測定値
â : 予測値
誤差は「(予測値:â)ー(実測値/ 測定値:y)」で統一しています。
誤差率を示すものはRMSPE以外は百分率(%)で統一しています。
実測値/測定値と予測値って?
実測値・予測値を推算式の研究に当てはめると、実測値/測定値が正しいCCr・GFRなので蓄尿やイヌリンを使って測定した「正しい腎機能」。それに対して、予測値は推算式(cockcroft-gault式など)を使って算出した数値で、eGFR(Estimate Glomerular Filtration Rate)/eCCr(Estimate Creatinine Clearance)が当てはまります。
ME(Mean Error:平均誤差)
予測値と実測値の差の平均を算出した数値。
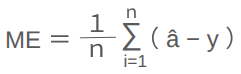
MAE(Mean Absolute Error:平均絶対誤差)
予測値と実測値の差の絶対値の平均。縦線に囲まれた部分は絶対値になります。
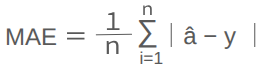
MSE(Mean Squared Error:平均二乗誤差)
予測値と実測値の差の2乗の平均値。数値を2乗にする方法は負の数をなくすためによく使う方法ですね。
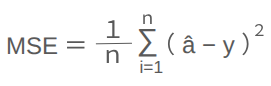
RMSE(Root Mean Squared Error:平均平方二乗誤差)
MSEの平方根。
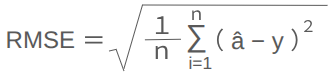
MPE(Mean Percentage Error:平均誤差率)
ここから「〜〜率シリーズ」。平均誤差(ME)を百分率(パーセント:%で示したもの)で示した指標。単位も「%」になります。
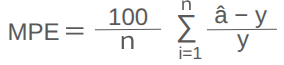
MAPE(Mean Absolute Percentage Error:平均絶対誤差率)
平均絶対誤差(MAE)を百分率(パーセンテージ:%)で示した指標。

RMSPE(Root Mean Squared Percentage Error:平均平方二乗誤差率)
平均平方二乗誤差(RMSE)を割合で示した指標。他の「〜〜率」で示している式は100倍にしていることがありました(されていない式もあります)が、この式に関しては100倍にされているものが見当たらなかったので、割合のままにしてあります。
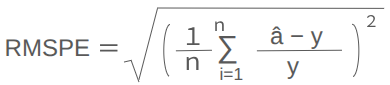
誤差の指標を分類に分けると
上記誤差を誤差と誤差率で分けてみました。視点としては誤差であるか、誤差率であるか。また、それぞれの指標になると思います。
| 平均誤差 | 平均絶対誤差 | 平均二乗誤差 | 平均平方二乗誤差 | |
| 誤差 | ME | MAE | MSE | RMSE |
| 誤差率 | MPE | MAPE | RMSPE |
比較するデータは?
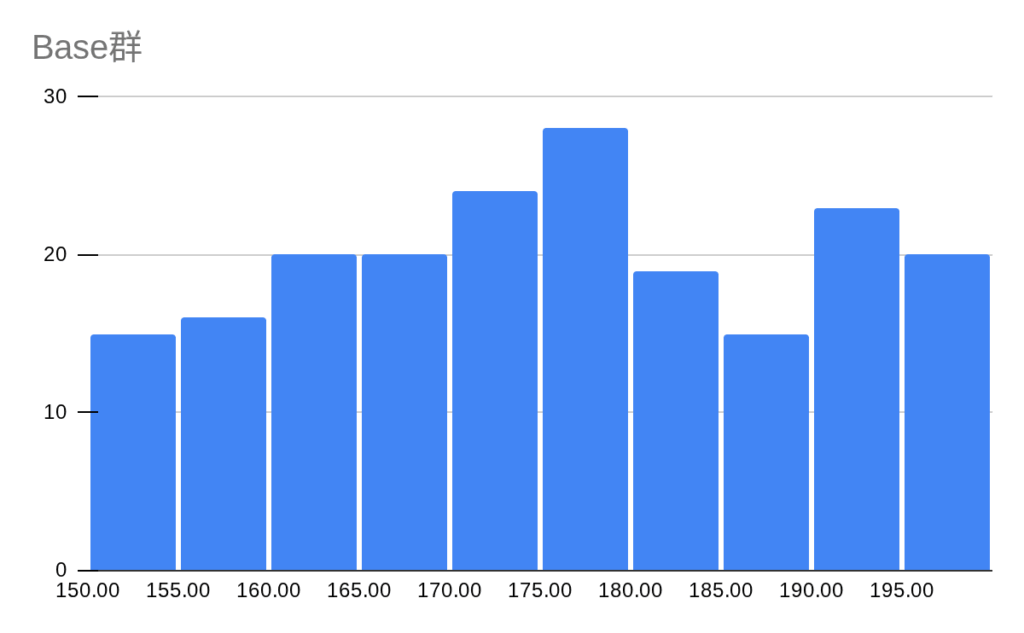
基準となる乱数の群=Base群を作成しました。下記がそのヒストグラムになります。
データ数:200
範囲:100〜150の小数点第一位までの乱数
今回比較するパターンを作っていきます。
Base群に対して変化量が多い群と少ない群を作成しています。作り方としてはBase群とBase群から100引いた群=Base低値群を作成しました。
1.正しい数値よりも一定値、高くなる(低くなる)パターン
Baseのデータ群が一律高くなる誤差=固定誤差を想定して作成しています。
作成方法は下記
Base一定値ずれる群(−10) = Base − 10
Base一定値ずれる群(+10) = Base + 10
3つの群のヒスㇳグラフを作成しておきました。
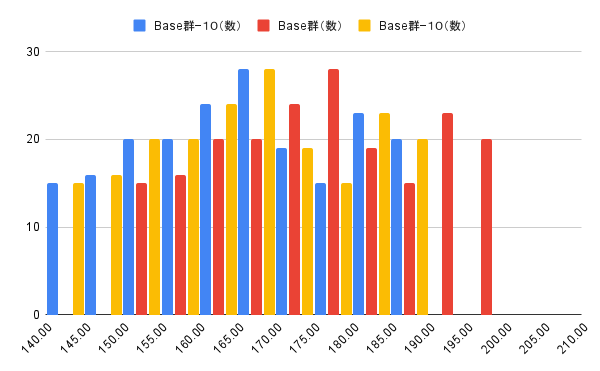
これとともに、Base群から100を引いた群でBase + 10群・Base − 10群を比べて比較しています。
2.正しい値が大きくなれば誤差が大きくなるパターン
Baseが大きくなるほど誤差が大きくなるパターン=比例誤差を想定して作成しています
作成方法は下記。
誤差徐々に増える群(影響小) = Base × 1.2
誤差徐々に増える群(影響中) = Base × 1.5
誤差徐々に増える群(影響大) = Base × 2.0
3.正しい数値よりもばらつきが大きくなるパターン
測定機のばらつきの大小の影響を見ることを想定して作成したパターンになります。正規分布に従う乱数を作成して、それをBaseに足しました。
作成方法は下記
ばらつきが小さい群 = Base+正規分布に従う乱数(平均:0 標準偏差:約30)
ばらつきが大きい群 = Base+正規分布に従う乱数(平均:0 標準偏差:約50)
4.外れ値の影響
外れ値の影響を想定して作成しています。
Baseから外れるものを大きい方に外れる外れ値と小さい方に外れる外れ値を作成しました。結果が負の数字となるものは作成したくないこともあり、割合で作成。
大きい方に外れる外れ値 = もともとのデータ + 100
小さい方に外れる外れ値 = もともとのデータ – 100
この外れ値の数を変えて作成しています。
外れ値も大きい方に外れる値が多いのか、少ない方に外れる値が多いのかにより、結果が変わってきます。ですので、同じ個数で同じように外れるもの、大きい方に外れる値が多い群、小さい方に外れる値が多い群を作成してみました
作成方法は下記4つを作成して、比較しました
①外れ値が少ないもの = 外れ値を2個作成
小さい方に外れる外れ値:1個
大きい方に外れる外れ値:1個 に作成
②外れ値が多いもの = 外れ値を10個作成(①のデータに加えて⑧個作成)
小さい方に外れる外れ値:5個
大きい方に外れる外れ値:5個 を作成
③大きい方に外れる外れ値が多いもの
大きい方に外れる外れ値を5個作成。
②で作成したデータから小さく外れる外れ値をもとに戻しました。
④小さく外れる外れ値が多いもの
小さく外れる外れ値を5個 作成
②で作成したデータから大きく外れる外れ値をもとに戻しました。
結果は?
1.正しい数値よりも一定値、高くなる(低くなる)パターン
Base群から10を足したり、引いたりすると下記。
差の平均値がずれることで、ME・MPEのみが正の方向、負の方向に変動します。逆にその他の指標では正の方向・負の方向のどちらにずれるかはわかりません。
良い意味で言えば、ME・MPEは差の平均値を算出していますので、全体的にどのように動いているかがわかりますが、正の方向/負の方向にズレたものを相殺していますので、一見の差が分かりづらいと言えるかもしれません。
逆にME・MAE以外の指標であれば、差が正の数になるか/ 負の数になるかは影響がなく比べることができます。
| ME | MAE | MSE | RMSE | |
| BASE+10 | 10 | 10 | 100 | 10 |
| 完全一致 | 0 | 0 | 0 | 0 |
| BASE−10 | -10 | 10 | 100 | 10 |
| MPE | MAPE | RMSPE | |
| BASE+10 | 5.72 | 5.72 | 0.06 |
| 完全一致 | 0.00 | 0.00 | 0.00 |
| BASE−10 | -5.72 | 5.72 | 0.06 |
これに対してBase群から100引いて変動する数字と母数の差を低くすると下記。
差の絶対値がME・MAE・MSE・RMSEは影響をうけませんが、「〜〜率」であるMPE・MAPE・RMSPEは影響が大きくなります。
| ME | MAE | MSE | RMSE | |
| BASE+10 | 10 | 10 | 100 | 10 |
| 完全一致 | 0 | 0 | 0 | 0 |
| BASE−10 | -10 | 10 | 100 | 10 |
| MPE | MAPE | RMSPE | |
| BASE+10 | 13.65 | 13.65 | 0.1365 |
| 完全一致 | 0 | 0 | 0 |
| BASE−10 | -13.65 | 13.65 | 0.1365 |
2.正しい値が大きくなれば誤差が大きくなるパターン
| ME | MAE | MSE | RMSE | |
| 完全一致 | 0 | 0 | 0 | 0 |
| Base × 1.2 | 35.16 | 35.16 | 1243.88 | 35.27 |
| Base × 1.5 | 87.91 | 87.91 | 7774.24 | 88.17 |
| Base × 2 | 175.81 | 175.81 | 31096.95 | 176.34 |
ME・MAE・MSEもいずれも大きくなるので変わりはしません
MPE・MAPE・RMSEは(Base × A)の影響を受けると仮定して、式を変換すると
MPE = (A−1)×100
MAPE = |A−1|×100
RMSPE = |A−1|
となります。これは、Baseや例数の影響を受けないという特性が確認できます。
ただし、今回は比例計算で算出しているので、このような結果。加速度的に上昇するようであれば、影響を受けることが予想されますので注意が必要だと思います。
良いか悪いかは調べたい事によるかもしれません。
| MPE | MAPE | RMSPE | |
| 完全一致 | 0 | 0 | 0 |
| Base × 1.2 | 20 | 20 | 0.2 |
| Base × 1.5 | 50 | 50 | 0.5 |
| Base × 2 | 100 | 100 | 1 |
3.正しい数値よりもばらつきが大きくなるパターン
今回はばらつきの平均値は0に設定してありますので、MEの変動はありません。つまり、マイナス方向の誤差とプラス方向の誤差で打ち消されるので、このパターンの誤差は確認することはできません。
ですが、その他の指標は変動しますし、ばらつきが大きくなればなるほど誤差が大きくなります。
| ME | MAE | MSE | RMSE | |
| 完全一致 | 0 | 0 | 0 | 0 |
| 差(SD=27.7) | 0 | 21.88 | 768.70 | 27.73 |
| 差(SD=51.0) | 0 | 40.12 | 2606.04 | 51.05 |
SD=標準偏差
| MPE | MAPE | RMSPE | |
| 完全一致 | 0 | 0 | 0 |
| 差(SD=27.7) | -0.117 | 12.51 | 0.001168 |
| 差(SD=51.0) | -0.395 | 23.10 | 0.003949 |
SD=標準偏差
4.外れ値の影響
外れ値の影響はいずれも受けますが、ME・MPEは差が大きい方向にずれる場合と差が少ない場合で異なり、互いに相殺されるため、同じように外れるというのでは異なる特性があります。
今回のデータでは「〜〜率」であるMPE・MAPE・RMASEの方が影響が少ないように見えますが、結局は上昇するので指標のみで外れ値の影響を除くことは難しいです。
| ME | MAE | MSE | RMSE | |
| 完全一致 | 0 | 0 | 0 | 0 |
| 外れ値:10個 | 0 | 5 | 500 | 22.36 |
| 外れ値:2個 | 0 | 2 | 200 | 14.14 |
| 大きい外れ値:5個 | 2.5 | 2.5 | 250 | 15.81 |
| 小さい外れ値:5個 | -2.5 | 2.5 | 250 | 15.81 |
| MPE | MAPE | RMSPE | |
| 完全一致 | 0 | 0 | 0 |
| 外れ値:10個 | 2.81 | 2.81 | 0.00055 |
| 外れ値:2個 | 0.015 | 1.14 | 0.00015 |
| 大きい外れ値:5個 | 1.38 | 1.38 | 0.01380 |
| 小さい外れ値:5個 | -1.43 | 1.43 | 0.01435 |
まとめると
ME・MPEは理論値/予測値と測定値の差が正になるか、負になるかの影響を受ける点で、他の指標とは異なります。また、比例誤差での特性も特徴でしょうか。
固定誤差・比例誤差・外れ値に分けて考えると分かりやすいと思い、下記まとめてみました。
下記を参考に指標を使い分けることが大切ですが、数字だけで判断するのは難しそう・・・
可能であれば指標を使いつつ、実際にグラフを作成するなど可視化することの方が正確性が増し良い結果となるとおもいます。
固定誤差のまとめ
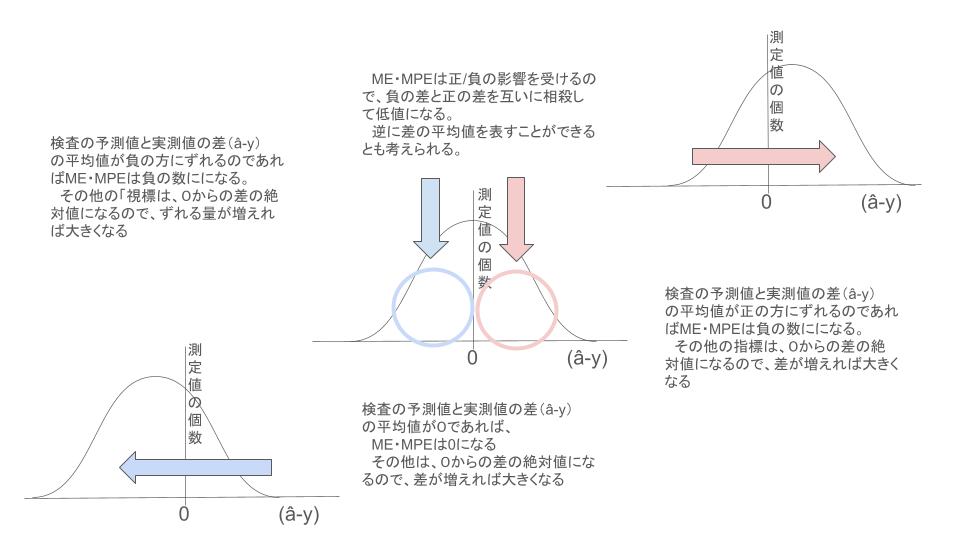
固定誤差(一定量ずれる差)の場合、ME・MPEは差が正の数になるか、負の数になるかの影響を受けます。
式でいうと
â(予測値)- y(実測値)
が負になるか、正になるかの影響を受け、それぞれに相殺される。それに対して、それ以外の指標では影響が受けにくい。平均値の算出はわかるが、正/負が均等になる場合には相殺されて、ME・MPEが低値になります。その他の指標では差が正/負が相殺されることはありませんので、絶対的な差が確認できます。差の平均値はわかりませんので、正の方向にずれるのか、負の方向にずれるのかはわかりません。
比例誤差のまとめ
比例誤差(Baseが大きければ大きいほど)の場合にはMPE・MAPE・RMASPEは症例数、Baseの数字の影響が受けにくい特性があります。比例であれば・・・
今回は調べていませんが、加速度的に上昇するのであれば、どうしても影響は強くなる事が予想されます。
外れ値のまとめ
ME・MPEは固定誤差の場合と同様に、正の方向に外れるのか/負の方向に外れるのかの影響を受けます。どちらにも影響がある場合にはそれぞれで相殺し合って数字は低値になります。
「〜〜率」であるMPE・MAPE・RMASEは影響の受ける量が減りますが、結局は影響を受けている。
ちなみに・・・
ShreadSheetやRを使って、関数で一発で計算しようと考えましたが、やり方がわからなかった。地道に計算するのが一番でしょうか・・・
参考)
データサイエンス塾 適切な誤差指標の選び方(参照:2025年8月3日)
https://analysis-navi.com/?p=2875
平均絶対パーセント誤差(MAPE:Mean absolute percentage error)とは?
(参照:2025年8月3日)
https://atmarkit.itmedia.co.jp/ait/articles/2106/09/news028.html#:~:text=%E6%A9%9F%E6%A2%B0%E5%AD%A6%E7%BF%92%E3%81%AB%E3%81%8A%E3%81%91%E3%82%8B%E5%B9%B3%E5%9D%87%E7%B5%B6%E5%AF%BE,%E5%87%BA%E5%8A%9B%E3%81%99%E3%82%8B%E9%96%A2%E6%95%B0%E3%81%A7%E3%81%82%E3%82%8B%E3%80%82
データサイエンス塾 適切な誤差指標の選び方(参照:2025年8月3日)
https://analysis-navi.com/?p=2875


コメント